Most Expected 180 Engineering Math Questions for GATE 2024 ( Part 10)

 Dear Students 

how are you ? hope part 9  for most excepted question for engineering math's has helped you lot. 

here we will discuss   Most Expected 180 Engineering Math Questions for GATE 2024 ( Part  10)

1. Consider the following two statements with respect to the matrices Am x n, Bn x m, Cn x n, Dn x n.

Statement 1 : tr(AB) = tr(BA)

Statement 2 : tr(CD) = tr(DC)

where tr( ) represents the trace of a matrix. Which one of the following holds? 

(A) Statement 1 is correct and Statement 2 is wrong

(B) Statement 1 is wrong and Statement 2 is correct

(C) Both Statement 1 and Statement 2 are correct

(D) Both Statement 1 and Statement 2 are wrong

Solution: Correct answer is (C).

2. Consider the functions 

I. e-x

II. x2 – sin x

III. √ (x3 + 1) 

Which of the above functions is/are increasing everywhere in [0,1]?

(A) III only

(B) II and III only

(C) II only

(D) I and III only

Solution: Correct answer is (A)

3. Choose the most appropriate equation for the function drawn as a thick line, in the plot below. 

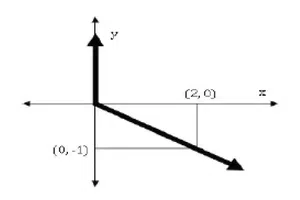
GATE CSE 2015

(A) x = y – |y|

(B) x = -(y – |y|)

(C) x = y + |y|

(D) x = -(y + |y|)

Solution: Correct answer is (B)

4. Consider a random variable X that takes values + 1 and-1 with probability 0.5 each. The values of the cumulative distribution function F(x) at x = – 1 and + 1 are

(A) 0 and 0.5

(B) 0 and 1

(C) 0.5 and 1

(D) 0.25 and 0.75

Solution: Correct answer is (C)

5. Consider the function f(x) = sin(x) in the interval [π/4, 7π/4]. The number and location(s) of the local minima of this function are 

(A) Two, at π/2 and 3π/2

(B) One, at 3π/2

(C) One, at π/2

(D) Two, at π/4 and 3π/2

Solution: Correct answer is (D)

6.

For a linear programming problem, which one of the following statements is FALSE?

1. If a constraint is an equality, then the corresponding dual variable is unrestricted in sign
2. Both primal and its dual can be infeasible
3. If primal is unbounded, then its dual is infeasible
4. Even if both primal and dual are feasible, the optimal values of the primal and the dual can differ

Answer (d)

7.

Let X be the number of heads in 4 tosses of a fair coin by Person 1 and let Y be the number of heads in 4 tosses of a fair coin by Person 2. Assume that all the tosses are independent. Then the value of P(X = Y ) correct up to three decimal places is ________

1. 0.272 to 0.274
2. 0.275 to 0.300
3. 0.300 to 0.305
4. None of the above

Answer (a)

8.An urn contains four balls, each ball having equal probability of being white or black. Three black balls are added to the urn. The probability that five balls in the urn are black is

1. 2/7
2. ⅜
3. ½
4. 5/7

Answer (b)

9 Let X be a square matrix. Consider the following two statements on X.

I. X is invertible.

II. Determinant of X is non-zero.

Which one of the following is TRUE?

1. I implies II; II does not imply I
2. II implies I; I does not imply II
3. I does not imply II; II does not imply I
4. I and II are equivalent statements

Answer (d)

10  The number of divisors of 2100 is ___________

1. 36
2. 35
3. 70
4. 30

Answer (a)

11. Consider the following statements:

S1: The sum of two singular n x n matrices may be non-singular

S2: The sum of two n x n non-singular matrices may be singular

Which of the following statements is correct?

1. S1 and S2 are both true
2. S1 is true, S2 is false
3. S1 is false, S2 is true
4. S1 and S2 are both false

Answer (a)

12. Consider the following set of equations

x + 2y = 5

4x + 8y = 12

3x + 6y + 3z = 15

This set

1. Has a unique solution
2. Has no solution
3. Has finite number of solutions
4. Has infinite number of solutions

Answer (b)

13.Consider the system, each consisting of m linear equations in variables.

I. If , then all such system have a solution

II. If , then none of these systems has a solution

III. If , then there exists a system which has a solution

Which one of the following is CORRECT?

1. I, II, and II are true
2. Only II and III are true
3. Only III is true
4. None of them are true

Answer (c)

14. 500 students are taking one or more courses out of chemistry, physics and mathematics. Registration records indicate course enrolment as follows: chemistry (329), physics (186), mathematics (295), chemistry and physics (83), chemistry and mathematics (217), and physics and mathematics (63), How many students are taking all 3 subjects?

1. 37
2. 43
3. 47
4. 53

Answer (d)

15. Three fair cubical dice are thrown simultaneously. The probability that all three dice have the same number of dots on the faces showing up is (up to third decimal place) ________.

1. 0.027
2. 0.050
3. 0.27
4. 0.50

Answer (a)

16 .The second moment of a Poisson-distributed random variable is 2. Then the mean of the random variable is ______.

1. 0
2. 1
3. 5
4. 10

Answer (b)

17. Let the random variable X represent the number of times a fair coin needs to be tossed till two consecutive heads appear for the first time. The expectation of X is _______.

1. 5
2. 6
3. 10
4. 11

Answer (b)

18. Let X∈{0,1} and Y∈{0,1} be two independent binary random variables. If P(X=0)=p

and P(Y=0)=q, then P(X+Y≥1) is equal to __________.

1. pq + (1 – p)(1 – q)
2. pq
3. p(1 – q)
4. 1 – pq

Answer (d)

Most Expected 180 Engineering Math Questions for GATE 2024 ( Part 9)

 Dear Students 

how are you ? hope part 8  for most excepted question for engineering math's has helped you lot. 

here we will discuss   Most Expected 180 Engineering Math Questions for GATE 2024 ( Part  9)

Most Expected 180 Engineering Math Questions for GATE 2024 ( Part 8)

  Dear Students 

how are you ? hope part 7  for most excepted question for engineering math's has helped you lot. 

here we will discuss   Most Expected 180 Engineering Math Questions for GATE 2024 ( Part  8)

Most Expected 180 Engineering Math Questions for GATE 2024 ( Part 7)

  Dear Students 

how are you ? hope part 6  for most excepted question for engineering math's has helped you lot. 

here we will discuss   Most Expected 180 Engineering Math Questions for GATE 2024 ( Part  7)